Stimulated and spontaneous emission
In 1916, Einstein showed that Planck's radiation law could be derived from a semi-classical, statistical treatment of photons and atoms, which implies a relation between the rates at which atoms emit and absorb photons. The condition follows from the assumption that light is emitted and absorbed by atoms independently, and that the thermal equilibrium is preserved by interaction with atoms. Consider a cavity in thermal equilibrium and filled with electromagnetic radiation and atoms that can emit and absorb that radiation. Thermal equilibrium requires that the energy density  of photons with frequency
of photons with frequency  (which is proportional to their number density) is, on average, constant in time; hence, the rate at which photons of any particular frequency are emitted must equal the rate of absorbing them.
(which is proportional to their number density) is, on average, constant in time; hence, the rate at which photons of any particular frequency are emitted must equal the rate of absorbing them.
 of photons with frequency
of photons with frequency  (which is proportional to their number density) is, on average, constant in time; hence, the rate at which photons of any particular frequency are emitted must equal the rate of absorbing them.
(which is proportional to their number density) is, on average, constant in time; hence, the rate at which photons of any particular frequency are emitted must equal the rate of absorbing them.
Einstein began by postulating simple proportionality relations for the different reaction rates involved. In his model, the rate  for a system to absorb a photon of frequency
for a system to absorb a photon of frequency  and transition from a lower energy
and transition from a lower energy  to a higher energy
to a higher energy 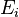 is proportional to the number
is proportional to the number  of atoms with energy
of atoms with energy  and to the energy density
and to the energy density  of ambient photons with that frequency,
of ambient photons with that frequency,
 for a system to absorb a photon of frequency
for a system to absorb a photon of frequency  and transition from a lower energy
and transition from a lower energy  to a higher energy
to a higher energy 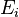 is proportional to the number
is proportional to the number  of atoms with energy
of atoms with energy  and to the energy density
and to the energy density  of ambient photons with that frequency,
of ambient photons with that frequency,
where  is the rate constant for absorption. For the reverse process, there are two possibilities: spontaneous emission of a photon, and a return to the lower-energy state that is initiated by the interaction with a passing photon. Following Einstein's approach, the corresponding rate
is the rate constant for absorption. For the reverse process, there are two possibilities: spontaneous emission of a photon, and a return to the lower-energy state that is initiated by the interaction with a passing photon. Following Einstein's approach, the corresponding rate  for the emission of photons of frequency
for the emission of photons of frequency  and transition from a higher energy
and transition from a higher energy 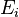 to a lower energy
to a lower energy  is
is
 is the rate constant for absorption. For the reverse process, there are two possibilities: spontaneous emission of a photon, and a return to the lower-energy state that is initiated by the interaction with a passing photon. Following Einstein's approach, the corresponding rate
is the rate constant for absorption. For the reverse process, there are two possibilities: spontaneous emission of a photon, and a return to the lower-energy state that is initiated by the interaction with a passing photon. Following Einstein's approach, the corresponding rate  for the emission of photons of frequency
for the emission of photons of frequency  and transition from a higher energy
and transition from a higher energy 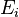 to a lower energy
to a lower energy  is
is
where  is the rate constant for emitting a photon spontaneously, and
is the rate constant for emitting a photon spontaneously, and  is the rate constant for emitting it in response to ambient photons (induced or stimulated emission). In thermodynamic equilibrium, the number of atoms in state i and that of atoms in state j must, on average, be constant; hence, the rates
is the rate constant for emitting it in response to ambient photons (induced or stimulated emission). In thermodynamic equilibrium, the number of atoms in state i and that of atoms in state j must, on average, be constant; hence, the rates  and
and  must be equal. Also, by arguments analogous to the derivation of Boltzmann statistics, the ratio of
must be equal. Also, by arguments analogous to the derivation of Boltzmann statistics, the ratio of  and
and  is
is  where
where  are the degeneracy of the state i and that of j, respectively,
are the degeneracy of the state i and that of j, respectively,  their energies, k the Boltzmann constant and T the system's temperature. From this, it is readily derived that
their energies, k the Boltzmann constant and T the system's temperature. From this, it is readily derived that  and
and
 is the rate constant for emitting a photon spontaneously, and
is the rate constant for emitting a photon spontaneously, and  is the rate constant for emitting it in response to ambient photons (induced or stimulated emission). In thermodynamic equilibrium, the number of atoms in state i and that of atoms in state j must, on average, be constant; hence, the rates
is the rate constant for emitting it in response to ambient photons (induced or stimulated emission). In thermodynamic equilibrium, the number of atoms in state i and that of atoms in state j must, on average, be constant; hence, the rates  and
and  must be equal. Also, by arguments analogous to the derivation of Boltzmann statistics, the ratio of
must be equal. Also, by arguments analogous to the derivation of Boltzmann statistics, the ratio of  and
and  is
is  where
where  are the degeneracy of the state i and that of j, respectively,
are the degeneracy of the state i and that of j, respectively,  their energies, k the Boltzmann constant and T the system's temperature. From this, it is readily derived that
their energies, k the Boltzmann constant and T the system's temperature. From this, it is readily derived that  and
and
The A and Bs are collectively known as the Einstein coefficients.
Einstein could not fully justify his rate equations, but claimed that it should be possible to calculate the coefficients  ,
,  and
and  once physicists had obtained "mechanics and electrodynamics modified to accommodate the quantum hypothesis". In fact, in 1926,Paul Dirac derived the
once physicists had obtained "mechanics and electrodynamics modified to accommodate the quantum hypothesis". In fact, in 1926,Paul Dirac derived the  rate constants in using a semiclassical approach, and, in 1927, succeeded in deriving all the rate constants from first principles within the framework of quantum theory. Dirac's work was the foundation of quantum electrodynamics, i.e., the quantization of the electromagnetic field itself. Dirac's approach is also called second quantization or quantum field theory; earlier quantum mechanical treatments only treat material particles as quantum mechanical, not the electromagnetic field.
rate constants in using a semiclassical approach, and, in 1927, succeeded in deriving all the rate constants from first principles within the framework of quantum theory. Dirac's work was the foundation of quantum electrodynamics, i.e., the quantization of the electromagnetic field itself. Dirac's approach is also called second quantization or quantum field theory; earlier quantum mechanical treatments only treat material particles as quantum mechanical, not the electromagnetic field.
 ,
,  and
and  once physicists had obtained "mechanics and electrodynamics modified to accommodate the quantum hypothesis". In fact, in 1926,Paul Dirac derived the
once physicists had obtained "mechanics and electrodynamics modified to accommodate the quantum hypothesis". In fact, in 1926,Paul Dirac derived the  rate constants in using a semiclassical approach, and, in 1927, succeeded in deriving all the rate constants from first principles within the framework of quantum theory. Dirac's work was the foundation of quantum electrodynamics, i.e., the quantization of the electromagnetic field itself. Dirac's approach is also called second quantization or quantum field theory; earlier quantum mechanical treatments only treat material particles as quantum mechanical, not the electromagnetic field.
rate constants in using a semiclassical approach, and, in 1927, succeeded in deriving all the rate constants from first principles within the framework of quantum theory. Dirac's work was the foundation of quantum electrodynamics, i.e., the quantization of the electromagnetic field itself. Dirac's approach is also called second quantization or quantum field theory; earlier quantum mechanical treatments only treat material particles as quantum mechanical, not the electromagnetic field.
Einstein was troubled by the fact that his theory seemed incomplete, since it did not determine the direction of a spontaneously emitted photon. A probabilistic nature of light-particle motion was first considered by Newton in his treatment of birefringence and, more generally, of the splitting of light beams at interfaces into a transmitted beam and a reflected beam. Newton hypothesized that hidden variables in the light particle determined which path it would follow. Similarly, Einstein hoped for a more complete theory that would leave nothing to chance, beginning his separation from quantum mechanics. Ironically, Max Born's probabilistic interpretation of the wave function was inspired by Einstein's later work searching for a more complete theory.

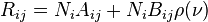

No comments:
Post a Comment