Experimental checks on photon mass
The photon is currently understood to be strictly massless, but this is an experimental question. If the photon is not a strictly massless particle, it would not move at the exact speed of light in vacuum, c. Its speed would be lower and depend on its frequency. Relativity would be unaffected by this; the so-called speed of light, c, would then not be the actual speed at which light moves, but a constant of nature which is the maximum speed that any object could theoretically attain in space-time. Thus, it would still be the speed of space-time ripples (gravitational waves and gravitons), but it would not be the speed of photons.
A massive photon would have other effects as well. Coulomb's law would be modified and the electromagnetic field would have an extra physical degree of freedom. These effects yield more sensitive experimental probes of the photon mass than the frequency dependence of the speed of light. If Coulomb's law is not exactly valid, then that would cause the presence of an electric field inside a hollow conductor when it is subjected to an external electric field. This thus allows one to test Coulomb's law to very high precision. A null result of such an experiment has set a limit of m ≲ 10−14 eV/c2.
Sharper upper limits have been obtained in experiments designed to detect effects caused by the galactic vector potential. Although the galactic vector potential is very large because the galactic magnetic field exists on very long length scales, the magnetic field is only observable if the photon is massless. In case of a massive photon, the mass term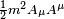 
would affect the galactic plasma. The fact that no such effects are seen implies an upper bound on the photon mass of m < 3×10−27 eV/c2. The galactic vector potential can also be probed directly by measuring the torque exerted on a magnetized ring. Such methods were used to obtain the sharper upper limit of 10−18eV/c2 (the equivalent of 1.07×10−27 atomic mass units) given by the Particle Data Group.
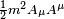would affect the galactic plasma. The fact that no such effects are seen implies an upper bound on the photon mass of m < 3×10−27 eV/c2. The galactic vector potential can also be probed directly by measuring the torque exerted on a magnetized ring. Such methods were used to obtain the sharper upper limit of 10−18eV/c2 (the equivalent of 1.07×10−27 atomic mass units) given by the Particle Data Group.
These sharp limits from the non-observation of the effects caused by the galactic vector potential have been shown to be model dependent. If the photon mass is generated via the Higgs mechanism then the upper limit of m≲10−14 eV/c2 from the test of Coulomb's law is valid.
Photons inside superconductors do develop a nonzero effective rest mass; as a result, electromagnetic forces become short-range inside superconductors.
No comments:
Post a Comment